The Coefficient of Form shows the relationship between the actual form of the ship and the dimensions of the ship.
Waterplane Area Coefficient (Cw)
It is the ratio of the actual area of the waterplane to the product of the length and breadth of the ship.
As seen below, the area of the ship’s waterplane is shown shaded and a rectangle having the same length and breadth of the ship:
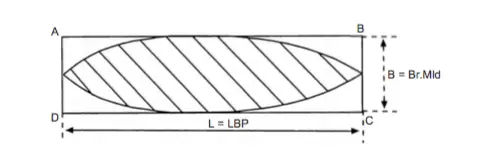
Coefficient of fineness (Cw) = Area of waterplane ÷ (Length x Breadth)
Example:
Q. Find the area of the waterplane of a ship 200 meters long, 30 meters beam, which has a coefficient of fineness of 0.800?
Ans. Area of waterplane = L x B x Cw
Area of waterplane = 200 x 30 x 0.8
Aw = 4800 sq m
Midship Section Area Coefficient (Cm)
It is the ratio of the actual area of the immersed portion of the ship’s midship section to the product of the breadth and the draught of the ship.
As seen below the shaded portion represents the area of the midships section to the waterline
WL, enclosed in a rectangle having the same breadth and depth.

Midship Coefficient (Cm) = Area of Immersed Midship Section (Am) ÷ (Breadth x Draught)
Hence,
Am = B x d x Cm
Block Coefficient (Cb)
The block coefficient of a ship at any particular draft is the ratio of the volume of displacement at that draft to the volume of a rectangular block having the same overall length, breadth, and depth.
In the figure below, the shaded portion represents the volume of the ship’s displacement at the draft concerned, enclosed in a rectangular block having the same overall length, breadth, and depth.
Block Coefficient (Cb) = Volume of displacement ÷ Volume of the block
Block Coefficient (Cb) = Volume of displacement ÷ ( L x B x draft)
∴ Volume of displacement = L x B x draft x Cb

Example
Q. A ship 64 meters long, 10 meters maximum beam, has a light draft of 1.5 meters and a load draft of 4 meters. The block coefficient of fineness is 0.600 at the light draft and 0.750 at the load draft. Find the deadweight.
Ans.
Light displacement = L x B x draft x Cb
= 64 x 10 x 1.5 x 0.600
= 576 cubic meters
Load displacement = L x B x draft x Cb
= 64 x 10 x 4 x 0.750
= 1920 cubic meters
Deadweight = Load displacement – Light displacement
= 1920 – 576 cubic meters
Deadweight = 1344 cubic meters
= 1344 x 1.025 tonnes
Deadweight = 1378 tonnes.
The Prismatic Coefficient (Cp)
The prismatic coefficient of a ship at any draft is the ratio of the volume of displacement at that draft to the volume of a prism having the same length as the ship and the same cross-sectional area as the ship’s midships area. The prismatic coefficient is used mostly by ship-model researchers.
In the figure below the shaded portion represents the volume of the ship’s displacement at the draft concerned, enclosed in a prism having the same length as the ship and a cross-sectional area equal to the ship’s midships area (Am).
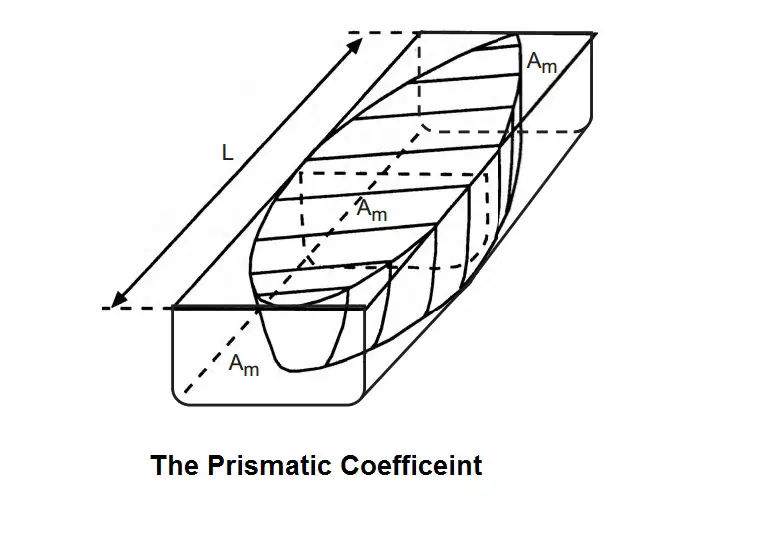
Prismatic coefficient (Cp) = Volume of ship ÷ Volume of prism
= Volume of ship ÷ (L x Am)
Volume of Ship = L x Am x Cp
Note that Cp is always slightly higher than Cb at each waterline.
Here how:
Cm x Cp = [Am ÷ (B x d)] x [Volume of ship ÷ (L x Am)]
= Volume of ship ÷ (L x B x d)
= Cb
Cm x Cp = Cb
or
Cp = Cb ÷ Cm
Having described exactly what Cw, Cb, Cm, and Cp are, it would be useful to know what their values would be for several ship types. For most merchant vessels, the coefficients are usually rounded off to three decimal places. However, for very large vessels such as supertankers or ULCCs, they are rounded off to four decimal places. First of all, it must be remembered that all of these form coefficients will never be more than
unity. To be so is not physically possible.
For the Cb values at fully loaded drafts Table below gives good typical values.

Is so wonderful
Cb is always higher then CP at each waterline , please check
Because in block coefficient formula we have B & T of the vessel and in CP formula we have midship section . And because of this there are transverse section curves and due to this Transverse Sections if you calculate this Cp area & compare it with Cb area at midship the values will be different.
Hance Cb will always be greater at different water line in comparison to Cp
I think it was well explained in the article.
We know that,
Cb = Volume ÷ ( L x B x draft)
Cp = Volume ÷ (L x Am)
Cm = Am ÷ (B x d)
From this,
Cm x Cp
=(Am ÷ (B x d)) x (Volume ÷ (L x Am)) <—The Am cancelled out
=Volume ÷ L x B x d <—–What we're left with is the formula of Cb
Therefore, we can conclude that Cm x Cp = Cb
or Cp= Cb ÷ Cm
Given the nature of these coefficients being ratio less than 1, we can deduce that Cp will be greater at each waterline by a factor of Cm
eg, if Cb=0.8, Cm = 0.9
Cp = 0.8/0.9
=0.8889